3 单腿的运动学与静力学

3.1 旋转矩阵与齐次变换矩阵

旋转矩阵可以表示由旋转变换得到的坐标系，齐次变换矩阵可以表示旋转+平移运动得到的坐标系。

$$\overrightarrow{OP}=x_s\cdot {\hat{\mathbf{x}}}_s+y_s\cdot {\hat{\mathbf{y}}}_s=x_b\cdot {\hat{\mathbf{x}}}_b+y_b\cdot {\hat{\mathbf{y}}}_b+\overrightarrow{O{O}^{\prime }}$$

引入齐次坐标，点的坐标末尾添加一个元素“1”，向量的坐标末尾添加一个元素“0”。

$$\left[\begin{array}{c}\overrightarrow{OP}\\ 0\end{array}\right]=\left[\begin{array}{ccc}{\hat{\mathbf{x}}}_s& {\hat{\mathbf{y}}}_s& \begin{array}{c}0\\ 0\end{array}\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}{x}_s\\ y_s\\ 1\end{array}\right]-\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]=\left[\begin{array}{ccc}{\hat{\mathbf{x}}}_b& {\hat{\mathbf{y}}}_b& \overrightarrow{O{O}^{\prime }}\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}{x}_b\\ y_b\\ 1\end{array}\right]-\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$$

其中：${\hat{\mathbf{x}}}_s=\left[\begin{array}{c}1\\ 0\end{array}\right]$，${\hat{\mathbf{y}}}_s=\left[\begin{array}{c}0\\ 1\end{array}\right]$，${\hat{\mathbf{x}}}_b=\left[\begin{array}{c}\cos \theta \\ \sin \theta \end{array}\right]$，${\hat{\mathbf{y}}}_b=\left[\begin{array}{c}-\sin \theta \\ \cos \theta \end{array}\right]$，则有

$$\left[\begin{array}{c}{x}_s\\ y_s\\ 1\end{array}\right]=\left[\begin{array}{ccc}\begin{array}{c}\cos \theta \\ \sin \theta \end{array}& \begin{array}{c}-\sin \theta \\ \cos \theta \end{array}& \overrightarrow{O{O}^{\prime }}\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}{x}_b\\ y_b\\ 1\end{array}\right]={\mathbf{T}}_{sb}\cdot \left[\begin{array}{c}{x}_b\\ y_b\\ 1\end{array}\right]$$

即：

$${\mathbf{T}}_{sb}=\left[\begin{array}{cc}{\mathbf{R}}_{sb}& \overrightarrow{O{O}^{\prime }}\\ 0_{1\times 2}& 1\end{array}\right]$$

为齐次变换矩阵。

在三维空间中则增加了一个维度，齐次变换矩阵也变为了 4x4 矩阵。

3.2 三维空间中机器人单腿的正向运动学

由三个关节的旋转角度求足部坐标。

3.2.1 坐标系

存在四个坐标系。

• 坐标系 $\{0\}$：与机身固定
• 坐标系 $\{1\}$：髋关节，绕其 $x$ 轴转动
• 坐标系 $\{2\}$：大腿关节，绕其 $y$ 轴转动，其 $z$ 轴与大腿重合
• 坐标系 $\{3\}$：小腿关节，绕其 $y$ 轴转动，其 $z$ 轴与小腿重合

其中，坐标系 $\{0\}$、$\{1\}$ 、 $\{2\}$ 的原点 $O_0$、$O_1$、$O_2$ 重合。$\overrightarrow{O_2{O}_3}=\left[\begin{array}{c}0\\ l_1\\ l_2\end{array}\right]$，其中 $l_1$ 大小为 $l_{abad}$。

1. 由 $\{0\}$ 到 $\{1\}$

   只有旋转过程，因此

   $${\mathbf{T}}_{01}=\left[\begin{array}{cc}{\mathbf{R}}_{0}1& \overrightarrow{O_0{O}_1}\\ 0_{1\times 3}& 1\end{array}\right]=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& \cos {\theta }_1& -\sin {\theta }_1& 0\\ 0& \sin {\theta }_1& \cos {\theta }_1& 0\\ 0& 0& 0& 1\end{array}\right]$$

2. 由 $\{1\}$ 到 $\{2\}$

   同理

   $${\mathbf{T}}_{12}=\left[\begin{array}{cccc}\cos {\theta }_2& 0& \sin {\theta }_2& 0\\ 0& 1& 0& 0\\ -\sin {\theta }_2& 0& \cos {\theta }_2& 0\\ 0& 0& 0& 1\end{array}\right]$$

3. 由 $\{2\}$ 到 $\{3\}$

旋转同时考虑平移

$${\mathbf{T}}_{23}=\left[\begin{array}{cccc}\cos {\theta }_3& 0& \sin {\theta }_3& 0\\ 0& 1& 0& l_1\\ -\sin {\theta }_3& 0& \cos {\theta }_3& l_2\\ 0& 0& 0& 1\end{array}\right]$$

其中

而 $P$ 点在坐标系$\{3\}$的坐标：$\left[\begin{array}{c}{\mathbf{p}}_3\\ 1\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ -l_{\text{knee}}\\ 1\end{array}\right]$

则可以求出其在坐标系 $\{0\}$ 的坐标 ${\mathbf{p}}_0$：

$$\left[\begin{array}{c}{\mathbf{p}}_0\\ 1\end{array}\right]={\mathbf{T}}_{01}{\mathbf{T}}_{12}{\mathbf{T}}_{23}\left[\begin{array}{c}{\mathbf{p}}_3\\ 1\end{array}\right]$$ $$\left[\begin{array}{c}{x}_p\\ y_p\\ z_p\\ 1\end{array}\right]=\left[\begin{array}{c}{l}_3\sin ({\theta }_2+{\theta }_3)+l_2\sin {\theta }_2\\ -l_3\sin {\theta }_1\cos ({\theta }_2+{\theta }_3)+l_1\cos {\theta }_1-l_2\cos {\theta }_2\sin {\theta }_1\\ l_3\cos {\theta }_1\cos ({\theta }_2+{\theta }_3)+l_1\sin {\theta }_1+l_2\cos {\theta }_1\cos {\theta }_2\\ 1\end{array}\right]$$

3.3 三维空间中机器人单腿的逆向运动学

3.3.1 机身关节 ${\theta }_1$

​​

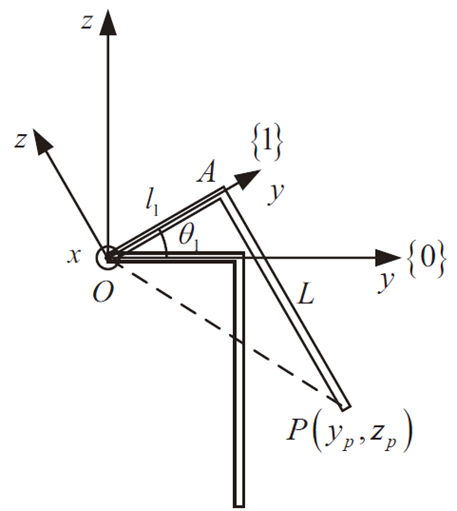
只考虑机身关节平面内的旋转矩阵

$$\left[\begin{array}{c}{y}_p\\ z_p\end{array}\right]=\left[\begin{array}{cc}\cos {\theta }_1& -\sin {\theta }_1\\ \sin {\theta }_1& \cos {\theta }_1\end{array}\right]\left[\begin{array}{c}{l}_1\\ -L\end{array}\right]$$

展开后可以计算

$$\{\begin{array}{rl}{y}_p& =l_1\cos {\theta }_1+L\sin {\theta }_1\\ z_p& =l_1\sin {\theta }_1-L\cos {\theta }_1\end{array}\Rightarrow \{\begin{array}{r}\frac{y_p}{\cos {\theta }_1}=l_1+L\tan {\theta }_1\\ \frac{z_p}{\cos {\theta }_1}=l_1\tan {\theta }_1-L\end{array}$$ $${\theta }_1=\arctan \left(\frac{z_p{l}_1+y_{p}L}{y_p{l}_1-z_{p}L}\right)$$

其中：$L=\sqrt{y_P^2+z_P^2-l_1^2}$

3.3.2 小腿关节 ${\theta }_3$

​​

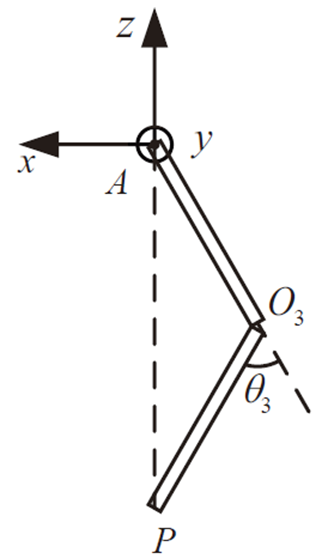
简单的平面几何求解

$$\cos \angle A{O}_{3}P=\frac{|\overrightarrow{O_{3}A}{|}^2+|\overrightarrow{O_{3}P}{|}^2-|\overrightarrow{AP}{|}^2}{2|\overrightarrow{O_{3}A}||\overrightarrow{O_{3}P}|}$$

由于 ${\theta }_3$ 是逆时针旋转，为负数，则

$${\theta }_3=-|{\theta }_3|=-\pi +\angle A{O}_{3}P=-\pi +\arccos \left(\frac{|\overrightarrow{O_{3}A}{|}^2+|\overrightarrow{O_{3}P}{|}^2-|\overrightarrow{AP}{|}^2}{2|\overrightarrow{O_{3}A}||\overrightarrow{O_{3}P}|}\right)$$

其中：$|\overrightarrow{AP}|=\sqrt{x_P^2+y_P^2+z_P^2-l_{\text{abad}}^2}$

3.3.3 大腿关节 ${\theta }_2$

将 $P$ 点坐标与前面求出来的 ${\theta }_1$ 与 ${\theta }_3$ 带入正向运动学的公式即可解出

$$\begin{array}{r}\tan {\theta }_2=\frac{a_1{m}_1+a_2{m}_2}{a_2{m}_1-a_1{m}_2}\end{array}$$

其中：$\{\begin{array}{rl}{a}_1& =y_p\sin {\theta }_1-z_p\cos {\theta }_1\\ a_2& =x_p\\ m_1& =l_3\sin {\theta }_3\\ m_2& =l_3\cos {\theta }_3+l_2\end{array}$

3.4 雅可比矩阵

对 $P$ 点在坐标系 $\{0\}$ 中的坐标 ${\vec{p}}_0$ 的三个值分别对时间求导，最后得到三个速度分量相对于角速度的系数矩阵，即雅可比矩阵。

$$\begin{array}{rl}{\dot{x}}_p& =0\cdot {\dot{\theta }}_1+[l_3\cos ({\theta }_2+{\theta }_3)+l_2\cos {\theta }_2]\cdot {\dot{\theta }}_2+l_3\cos ({\theta }_2+{\theta }_3)\cdot {\dot{\theta }}_3\\ & =J_{11}\cdot {\dot{\theta }}_1+J_{12}\cdot {\dot{\theta }}_2+J_{13}\cdot {\dot{\theta }}_3\end{array}$$ $$\begin{array}{rl}{\dot{y}}_p& =[-l_1\sin {\theta }_1-l_2\cos {\theta }_1\cos {\theta }_2-l_3\cos {\theta }_1\cos ({\theta }_2+{\theta }_3)]\cdot \dot{{\theta }_1}+[l_2\sin {\theta }_1\sin {\theta }_2+l_3\sin {\theta }_1\sin ({\theta }_2+{\theta }_3)]\cdot \dot{{\theta }_2}+l_3\sin {\theta }_1\sin ({\theta }_2+{\theta }_3)\cdot \dot{{\theta }_3}\\ & =J_{21}\cdot {\dot{\theta }}_1+J_{22}\cdot {\dot{\theta }}_2+J_{23}\cdot {\dot{\theta }}_3\end{array}$$ $$\begin{array}{rl}{\dot{z}}_p& =[l_1\cos {\theta }_1-l_2\sin {\theta }_1\cos {\theta }_2-l_3\sin {\theta }_1\cos ({\theta }_2+{\theta }_3)]\cdot \dot{{\theta }_1}+[-l_2\cos {\theta }_1\sin {\theta }_2-l_3\cos {\theta }_1\sin ({\theta }_2+{\theta }_3)]\cdot \dot{{\theta }_2}+[-l_3\cos {\theta }_1\sin ({\theta }_2+{\theta }_3)\cdot \dot{{\theta }_3}]\\ & =J_{31}\cdot {\dot{\theta }}_1+J_{32}\cdot {\dot{\theta }}_2+J_{33}\cdot {\dot{\theta }}_3\end{array}$$

整理成矩阵相乘：

$$\left[\begin{array}{c}{\dot{x}}_p\\ {\dot{y}}_p\\ {\dot{z}}_p\end{array}\right]=\left[\begin{array}{ccc}{J}_{11}& J_{12}& J_{13}\\ J_{21}& J_{22}& J_{23}\\ J_{31}& J_{32}& J_{33}\end{array}\right]\cdot \left[\begin{array}{c}{\dot{\theta }}_1\\ {\dot{\theta }}_2\\ {\dot{\theta }}_3\end{array}\right]=\mathbf{J}\cdot \left[\begin{array}{c}{\dot{\theta }}_1\\ {\dot{\theta }}_2\\ {\dot{\theta }}_3\end{array}\right]$$

也有

$$\left[\begin{array}{c}{\dot{\theta }}_1\\ {\dot{\theta }}_2\\ {\dot{\theta }}_3\end{array}\right]={\mathbf{J}}^{-1}\cdot \left[\begin{array}{c}{\dot{x}}_p\\ {\dot{y}}_p\\ {\dot{z}}_p\end{array}\right]$$

3.4.1 单腿静力学

假设机器人处于静止状态，整条腿的动能保持不变，即总功率为0。可以视为关节对腿做功功率 = 足端对地面做功功率

$$P_{关节对腿做功}=P_{足端对地面做功}$$

那么就有

$$\left[\begin{array}{ccc}{\tau }_1& {\tau }_2& {\tau }_3\end{array}\right]\cdot \left[\begin{array}{c}{\dot{\theta }}_1\\ {\dot{\theta }}_2\\ {\dot{\theta }}_3\end{array}\right]=\left[\begin{array}{ccc}{F}_x& F_y& F_z\end{array}\right]\cdot \left[\begin{array}{c}{\dot{x}}_p\\ {\dot{y}}_p\\ {\dot{z}}_p\end{array}\right]$$ $${\mathbf{\tau }}^{\mathrm{T}}\cdot \left[\begin{array}{c}{\dot{\theta }}_1\\ {\dot{\theta }}_2\\ {\dot{\theta }}_3\end{array}\right]={\mathbf{F}}^{\mathrm{T}}\cdot \mathbf{J}\cdot \left[\begin{array}{c}{\dot{\theta }}_1\\ {\dot{\theta }}_2\\ {\dot{\theta }}_3\end{array}\right]$$

即有

$$\mathbf{\tau }={\mathbf{J}}^{\mathrm{T}}\cdot \mathbf{F}$$